从入门到进阶共10本电子书（今日鸡汤会挽雕弓如满月）

点击上方“爬虫与数据挖掘”，进行关注

回复“书籍”即可获赠从入门到进阶共10本电子书

今

日

鸡

汤

会挽雕弓如满月，西北望，射天狼。

作者 | Tatan

译者 | 李洁

编辑 |

出品 | 数据之道

用快速分析、可视化和预测股票价格

1 前言

某天，我的一个朋友告诉我说，实现经济自由的关键是股票投资。虽然这是市场繁荣时期的真理，但如今业余交易股票仍然是一个有吸引力的选择。由于在线交易平台的便利性，涌现了许多自主价值投资者或家庭主妇交易员。甚至还有一些成功的故事和广告吹嘘有“快速致富计划”学习如何投资回报率高达 40% 甚至更高的股票。投资已成为当今职场人士的福音。

现在的问题是：哪些股票？如何分析股票？与其他股票相比，所选股票的回报和风险是什么？

本文的目标是让你了解使用快速简单的 代码分析股票的一种方法。只需花 12 分钟阅读这篇文章——最好自己完成一下。然后你就可以快速浏览到你的第一份金融分析报告。

为了开始学习和分析股票，我们将从快速查看历史股票价格开始。这将通过从 网络数据阅读器和雅虎财经中提取最新的股票数据来实现。然后，我们将尝试通过探索性分析，如相关性热图、 可视化以及使用线性分析和k最近邻（K ,KNN）的预测分析来查看数据。

2 加载雅虎财经数据集

网络数据阅读器（ web data ）是 库的一个扩展，用于与大多数最新的金融数据进行通信，包括雅虎财经、谷歌财经、 等资源。

我们将使用以下代码提取 Apple 的股票价格：

import pandas as pd
import datetime
import pandas_datareader.data as web
from pandas import Series, DataFrame
start = datetime.datetime(2010, 1, 1)
end = datetime.datetime(2017, 1, 11)
df = web.DataReader("AAPL", 'yahoo', start, end)
df.tail()

来源于雅虎财经的股票价格

这段代码将提取从 2010 年 1 月到 2017 年 1 月的 7 年的数据。你可以根据需要调整开始和结束日期。接下来的分析过程，我们将使用收盘价格，即股票在一天交易结束时的最终价格。

3 探索股票的移动平均值和收益率

在这个分析中，我们使用两个关键的测量指标来分析股票：移动平均值和回报率。

3.1 移动平均值：确定趋势

滚动平均 / 移动平均（MA）通过不断更新平均价格来平滑价格数据，有助于降低价格表中的“噪音”。此外，该移动平均线可能充当“阻力”，代表着股票的下跌和上升趋势，你可以从中预期它的未来趋势，不太可能偏离阻力点。

让我们开始写代码来得到滚动平均值:

close_px = df['Adj Close']
mavg = close_px.rolling(window=100).mean()

最后 10 个移动平均值

这将计算股票收盘价最后 100 个滑窗（100天）的移动平均值，并取每个滑窗的移动平均值。正如你所看到的，移动平均线在滑窗上稳步上升，并不遵循股票价格曲线的锯齿线。为了更好地理解，让我们用 来绘制它。我们将用移动平均线来绘制股票价格表。

%matplotlib inline
import matplotlib.pyplot as plt
from matplotlib import style
# Adjusting the size of matplotlib
import matplotlib as mpl
mpl.rc('figure', figsize=(8, 7))
mpl.__version__
# Adjusting the style of matplotlib
style.use('ggplot')
close_px.plot(label='AAPL')
mavg.plot(label='mavg')
plt.legend()

苹果股票移动平均价格(mavg)

移动平均使曲线平滑，显示股票价格的涨跌趋势。

在这张图表中，移动平均线显示了股票价格上升或下降的趋势。从逻辑上讲，你应该在股市低迷时买进，在股市上涨时卖出。

3.2 回报偏差:用于确定风险和收益

预期收益衡量投资收益概率分布的平均值或预期值。投资组合的预期回报是通过将每项资产的权重乘以其预期回报，再加上每项投资的价值来计算的。（摘自投资百科，）

你可以参考以下公式：

收益公式

根据这个公式，我们可以画出收益，如下。

rets = close_px / close_px.shift(1) - 1
rets.plot(label='return')

收益率

从逻辑上讲，我们理想的股票收益应该尽可能高且稳定。如果你是风险规避者（像我一样），你可能希望避开这种股票大六壬入门图解预测股票，因为你看到 2013 年下跌了 10%。这个决定很大程度上取决于你对股票的总体看法和对其他竞争对手股票的分析。

4 分析竞争对手股票

在这部分中，我们将分析一家公司相对于其竞争对手的表现。假设我们对科技公司感兴趣，并想比较一下这些巨头：苹果（Apple）、通用电气（GE）、谷歌（）、IBM 和微软（）。

dfcomp = web.DataReader(['AAPL', 'GE', 'GOOG', 'IBM', 'MSFT'],'yahoo',start=start,end=end)['Adj Close']

苹果、通用电气、谷歌、IBM 和微软的股价

你将会从雅虎财经的股票价格中得到一张相当整洁平滑的收盘价表。

4.1 相关性分析:竞争对手会互相影响吗？

我们可以通过运行 的百分比变化和相关函数来分析竞争关系。百分比变化将定义收益 ，找出与前一天相比价格变化的程度。了解相关性将有助于我们理解收益是否受其他股票收益的影响。

retscomp = dfcomp.pct_change()
corr = retscomp.corr()

让我们绘制散点图来观察 Apple 和 GE 的收益分布。

plt.scatter(retscomp.AAPL, retscomp.GE)
plt.xlabel('Returns AAPL')
plt.ylabel('Returns GE')

Apple 和 GE 的散点图

我们可以看到，GE 的收益和 Apple 的收益之间存在着微弱的正相关关系。似乎在大多数情况下， Apple 的回报率越高，GE 的回报率也就越高。

让我们通过绘制散点矩阵进一步改进我们的分析，以可视化竞争股票之间可能的相关性。在对角点从入门到进阶共10本电子书（今日鸡汤会挽雕弓如满月），我们将运行核密度估计( ,KDE)。KDE 是一个基本的数据平滑问题，它基于有限的数据样本对总体进行推断。它有助于生成对总体分布的估计。

pd.scatter_matrix(retscomp, diagonal='kde', figsize=(10, 10))

KDE 图和散点矩阵

从这里我们可以得到大多数股票之间的分布近似正相关。

为了证明正相关关系，我们将使用热图来可视化竞争股票之间的相关程度。注意颜色越浅代表这两只股票的相关性越强。

plt.imshow(corr, cmap='hot', interpolation='none')
plt.colorbar()
plt.xticks(range(len(corr)), corr.columns)
plt.yticks(range(len(corr)), corr.columns)

竞争股票之间相关性的热图

从散点矩阵和热图中我们可以发现，竞争股票之间有很大的相关性。然而，这可能并不能说明因果关系，只能说明科技行业的趋势而不能说明相互竞争的股票是如何相互影响的。

4.2 股票回报率和风险

除了相关性，我们还分析了每支股票的风险和回报。本例中我们提取的是回报的平均值（回报率）和回报的标准差（风险）。

plt.scatter(retscomp.mean(), retscomp.std())
plt.xlabel('Expected returns')
plt.ylabel('Risk')
for label, x, y in zip(retscomp.columns, retscomp.mean(), retscomp.std()):
    plt.annotate(label,xy = (x, y), xytext = (20, -20),
       textcoords = 'offset points', ha = 'right', va = 'bottom',
       bbox = dict(boxstyle = 'round,pad=0.5', fc = 'yellow', alpha = 0.5),
       arrowprops = dict(arrowstyle = '->', connectionstyle = 'arc3,rad=0'))

股票风险与收益的快速散点图

现在你可以看到这张关于竞争股票的风险和收益比较的清晰的图表。从逻辑上讲，你想要将风险最小化，并使收益最大化。因此，您需要为您的风险回报容忍度画一条线(红线)。然后，你将创建规则——购买红线以下的股票(微软、通用电气和 IBM)，卖出红线以上的股票(苹果和谷歌)。这条红线显示了您的期望值阈值和买进/卖出决策的基线。

5 预测股票价格 5.1 特征工程

我们将使用这三个机器学习模型来预测股票:简单线性分析、二次判别分析( ，QDA)和 K近邻(K ，KNN)。但首先我们需要设计一些特征：高-低百分比和百分比变化。

dfreg = df.loc[:,['Adj Close','Volume']]
dfreg['HL_PCT'] = (df['High'] — df['Low']) / df['Close'] * 100.0
dfreg['PCT_change'] = (df['Close'] — df['Open']) / df['Open'] * 100.0

生成的最终数据帧

5.2 预处理和交叉验证

在将数据放入预测模型之前，我们将按照以下步骤对数据进行清洗和处理：

1.删除缺失值

2.分离标签，我们要预测

3.缩放 X ，使每个样本都可以具有相同的线性回归分布。

4.最后，我们要找到近期 X 和早期 X （用于训练）的数据序列，用于模型生成和评估。

5.分离标签并标识为 Y。

6.分别通过交叉验证训练模型和测试

请参考以下的代码。

# Drop missing value
dfreg.fillna(value=-99999, inplace=True)
# We want to separate 1 percent of the data to forecast
forecast_out = int(math.ceil(0.01 * len(dfreg)))
# Separating the label here, we want to predict the AdjClose
forecast_col = 'Adj Close'
dfreg['label'] = dfreg[forecast_col].shift(-forecast_out)
X = np.array(dfreg.drop(['label'], 1))
# Scale the X so that everyone can have the same distribution for linear regression
X = preprocessing.scale(X)
# Finally We want to find Data Series of late X and early X (train) for model generation and evaluation
X_lately = X[-forecast_out:]
X = X[:-forecast_out]
# Separate label and identify it as y
y = np.array(dfreg['label'])
y = y[:-forecast_out]

5.3 模型生成-预测过程有意思的地方开始了

首先，让我们为我们的 -Learn 库 的导入添加以下代码：

from sklearn.linear_model import LinearRegression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import Ridge
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline

5.4 简单线性分析和二次判别分析

简单线性分析给出两个或多个变量之间的线性关系。当我们在两个变量中画关系图时，我们会得到一条直线。二次判别分析类似于简单线性分析，只是模型允许多项式(例如: x 平方)的生成并会产生曲线。

线性回归预测因变量(Y)为输出而自变量(X)为输入。在绘制过程中，我们会得到一条直线，如下图所示:

简单线性回归

以下是一篇相当干货的文章，它对线性回归进行了全面的回顾。

A ’s guide to in with -Learn

我们将导入并使用现有的 库，并通过选择 X 和 Y 训练集来训练模型。代码如下。

# Linear regression
clfreg = LinearRegression(n_jobs=-1)
clfreg.fit(X_train, y_train)
# Quadratic Regression 2
clfpoly2 = make_pipeline(PolynomialFeatures(2), Ridge())
clfpoly2.fit(X_train, y_train)
# Quadratic Regression 3
clfpoly3 = make_pipeline(PolynomialFeatures(3), Ridge())
clfpoly3.fit(X_train, y_train)

5.5 K最近邻(KNN)

KNN利用特征相似性来预测数据点的值。这保证了分配的新点与数据集中的点相似。为了找出相似点，我们提取这些点间的最小距离(例如：欧氏距离)。

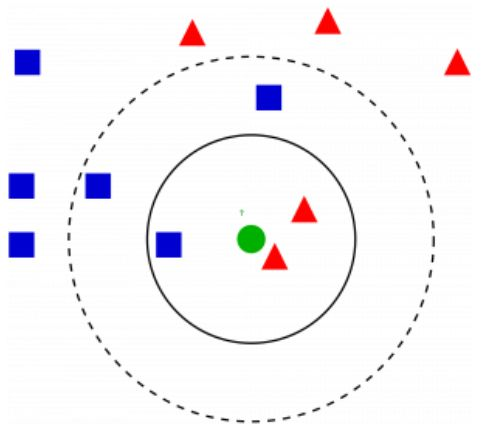
在 KNN 模型可视化中，你将会以 k 个数量的元素对问题元素进行分组

有关模型的详细资料，请参阅以下链接。这对加深你的理解非常有用。

to k- : (with in )

# KNN Regression
clfknn = KNeighborsRegressor(n_neighbors=2)
clfknn.fit(X_train, y_train)

5.6 评估

一种简单、快速、粗略的评估方法是在每个训练过的模型中使用 score 方法。score 可以得到测试数据集的 self.(X) 与 y 的平均精度。

confidencereg = clfreg.score(X_test, y_test)
confidencepoly2 = clfpoly2.score(X_test,y_test)
confidencepoly3 = clfpoly3.score(X_test,y_test)
confidenceknn = clfknn.score(X_test, y_test)
# results
('The linear regression confidence is ', 0.96399641826551985)
('The quadratic regression 2 confidence is ', 0.96492624557970319)
('The quadratic regression 3 confidence is ', 0.9652082834532858)
('The knn regression confidence is ', 0.92844658034790639)

结果显示大多数模型的精确性评分（>0.95）。然而，这并不意味着我们可以盲目地持有这些股票。仍然有许多问题需要考虑，特别是对于不同的公司来说从入门到进阶共10本电子书（今日鸡汤会挽雕弓如满月），随着时间的推移，它们的价格走势也会不同。

为了进行全面的测试，让我们输出一些股票的预测。

forecast_set = clf.predict(X_lately)
dfreg['Forecast'] = np.nan
#result
(array([ 115.44941187,  115.20206522,  116.78688393,  116.70244946,
        116.58503739,  115.98769407,  116.54315699,  117.40012338,
        117.21473053,  116.57244657,  116.048717  ,  116.26444966,
        115.78374093,  116.50647805,  117.92064806,  118.75581186,
        118.82688731,  119.51873699]), 0.96234891774075604, 18)

6 绘制预测图

根据预测值大六壬入门图解预测股票，我们将用现有的历史数据来可视化绘图。这将有助于我们可视化模型如何预测未来股票价格。

last_date = dfreg.iloc[-1].name
last_unix = last_date
next_unix = last_unix + datetime.timedelta(days=1)
for i in forecast_set:
    next_date = next_unix
    next_unix += datetime.timedelta(days=1)
    dfreg.loc[next_date] = [np.nan for _ in range(len(dfreg.columns)-1)]+[i]
dfreg['Adj Close'].tail(500).plot()
dfreg['Forecast'].tail(500).plot()
plt.legend(loc=4)
plt.xlabel('Date')
plt.ylabel('Price')
plt.show()

图形表示预测值

如图所示，蓝线显示了基于回归的股票价格预测。预测表明，经济衰退不会持续太久大六壬入门图解预测股票，然后就会复苏。因此，我们可以在经济低迷时买进股票，在经济好转时卖出。

7 未来的改进/挑战

为了进一步分析股票，这里有一些你可以实现的想法。这些想法将有助于对股票进行更全面的分析。如果需要更多的说明，请随时通知我。

代码

在公众号『数据之道』后台回复 “code”，可以获取本文的代码文件

• 上一篇： 风水堂：本法能很快掌握和应用
• 下一篇：（李向东）小六壬多功能转盘怎么用转盘用法